
【其他年金终值与现值】
1.年金分类
年金按照收付时点和方式的不同,可以分类为以下四种:
|
(1)普通年金 |
年金最基本形式,从第一期开始,在一定时期内每期期末等额收付的系列款项 |
|
(2)预付年金 |
从第一期开始,在一定时期内每期期初等额收付的系列款项 |
|
(3)递延年金 |
在第二期或第二期以后收付的系列款项,由普通年金递延形成 |
|
(4)永续年金 |
收付次数为无穷大时的普通年金 |
|
(1)普通年金 |
从第一期开始,在一定时期内每期期末等额收付的系列款项 |
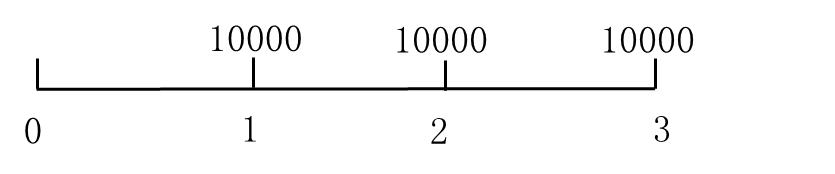
|
(2)预付年金 |
从第一期开始,在一定时期内每期期初等额收付的系列款项 |
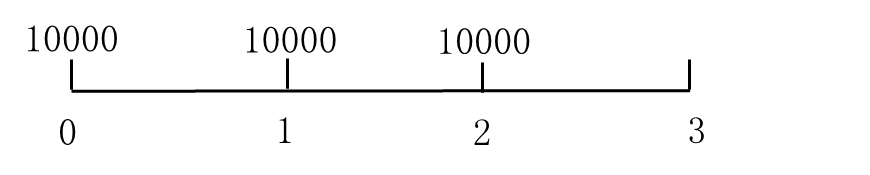
|
(3)递延年金 |
在第二期或第二期以后收付的系列款项,由普通年金递延形成 |

|
(4)永续年金 |
收付次数为无穷大时的普通年金 |
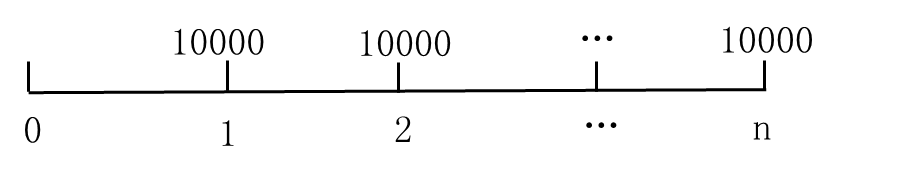
2.预付年金终值和现值
(1)终值

方法一:
普通年金的终值:F=A×(F/A,i,n)
预付年金的终值:F=A×(F/A,i,n)×(1+i)
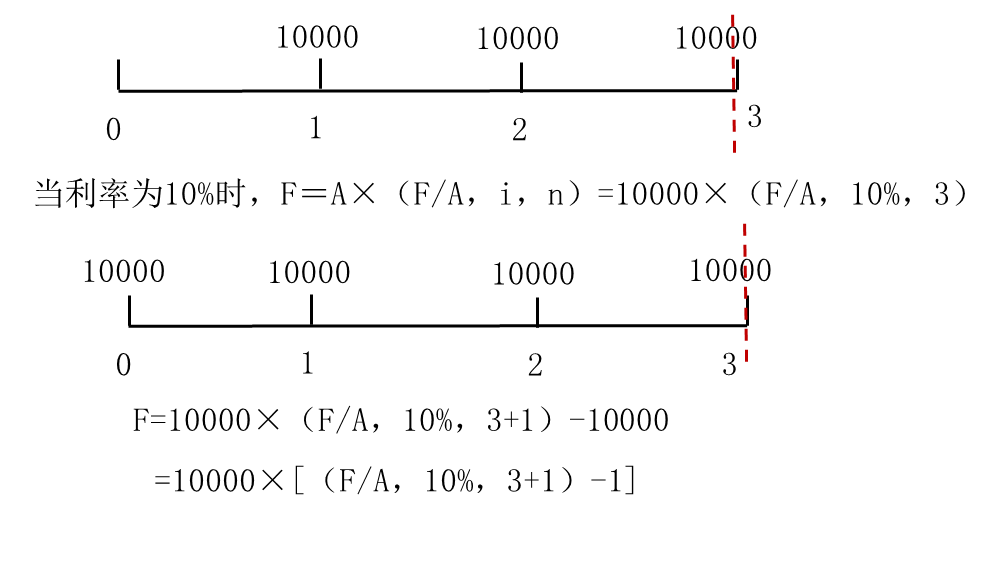
方法二:
普通年金的终值:F=A×(F/A,i,n)
预付年金的终值:F=A×[(F/A,i,n+1)-1]
(2)现值
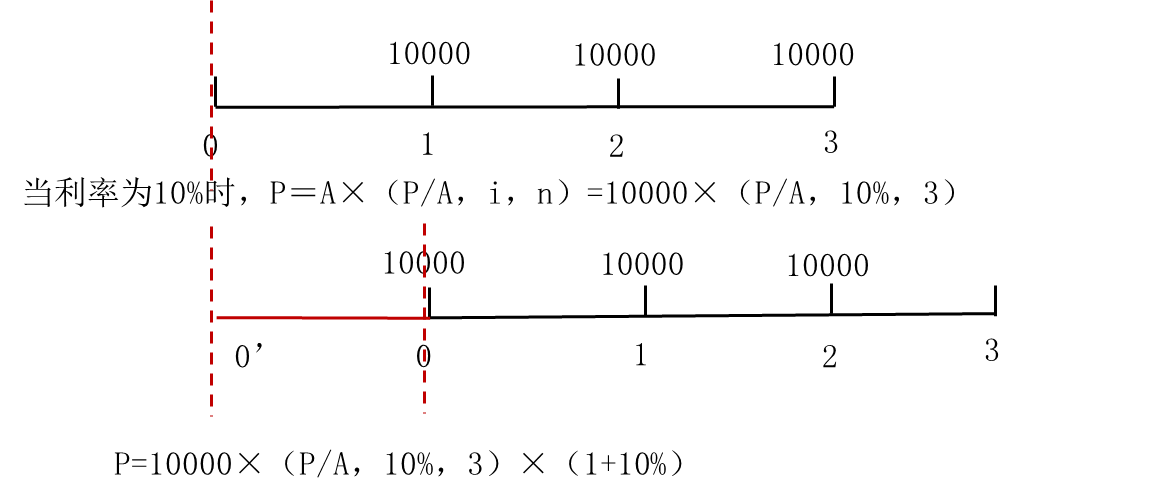
方法一:
普通年金的现值:P=A×(P/A,i,n)
预付年金的现值:P=A×(P/A,i,n)×(1+i)

方法二:
普通年金的现值:P=A×(P/A,i,n)
预付年金的现值:P=A×[(P/A,i,n-1)+1]
总结
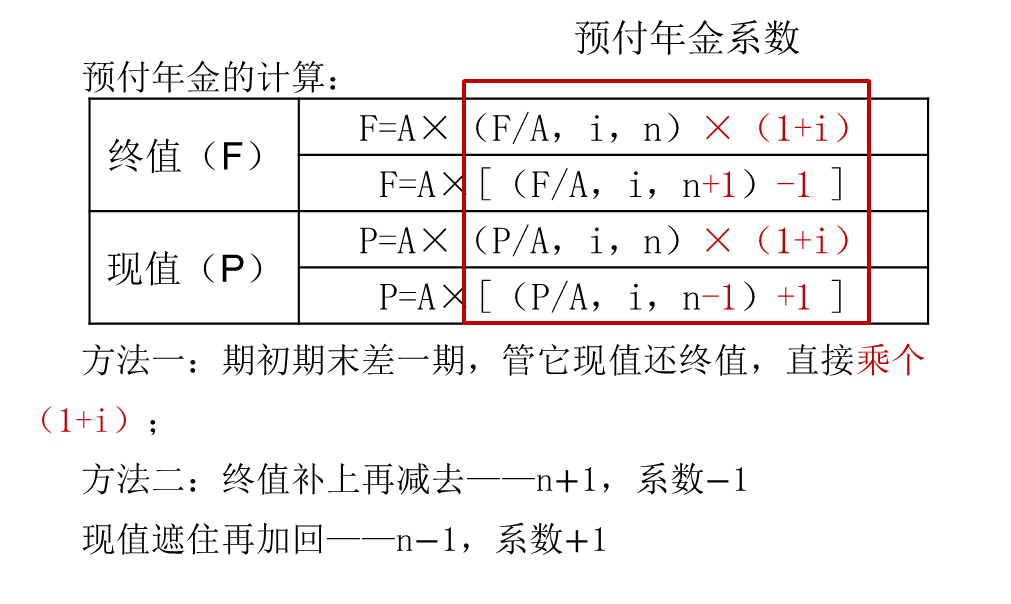
3.递延年金终值和现值
递延年金:在第二期或第二期以后收付的系列款项,由普通年金递延形成。
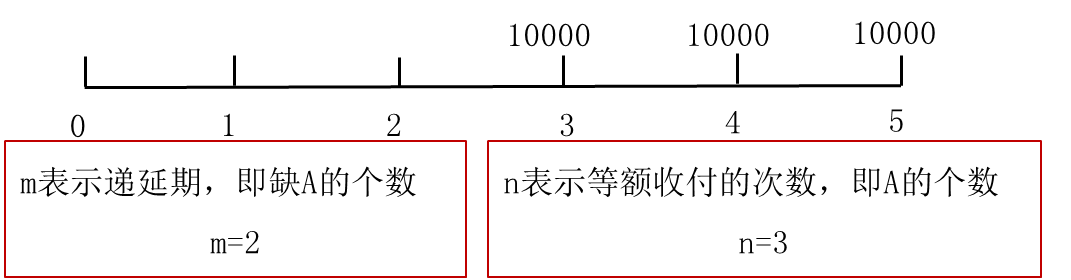
(1)终值
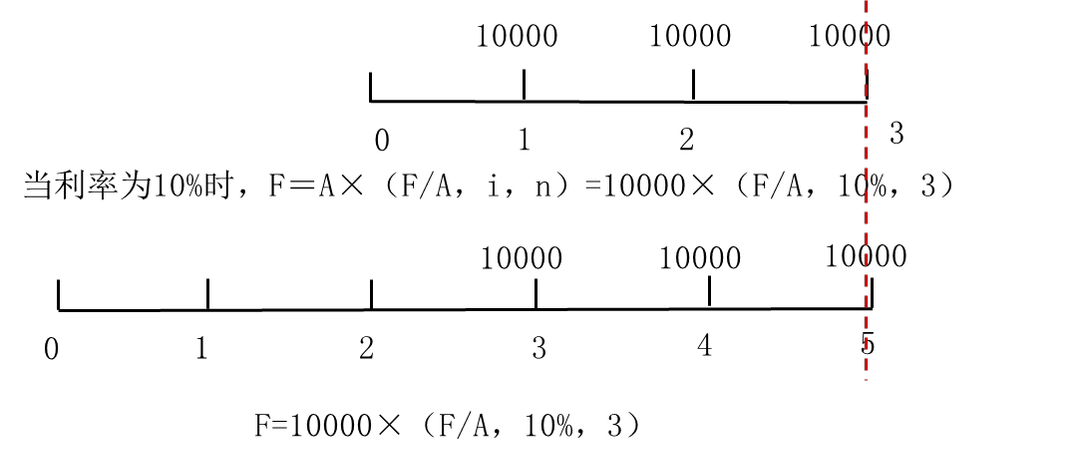
普通年金的终值:F=A×(F/A,i,n)
递延年金的终值:F=A×(F/A,i,n)
即终值不受递延期m的影响
(2)现值
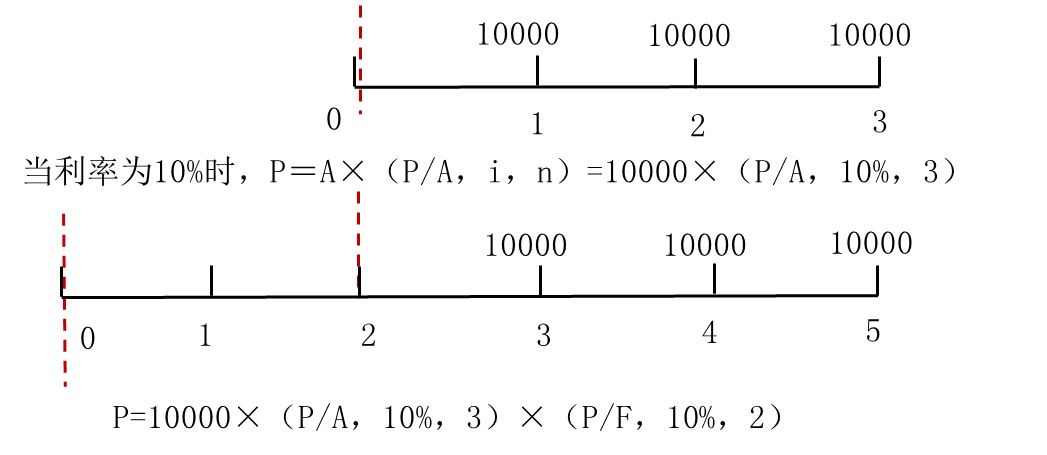
方法一(两次折现):年金折完复利折
P=A×(P/A,i,n)×(P/F,i,m)

方法二(先补后减):
P=A×(P/A,i,n+m)-A×(P/A,i,m)=A×[(P/A,i,n+m)-(P/A,i,m)]
递延年金的计算:
|
终值(F) |
F=A×(F/A,i,n) |
|
现值(P) |
P=A×(P/A,i,n)×(P/F,i,m) |
|
P=A×[(P/A,i,n+m)-(P/A,i,m)] |
方法一:两次折现——年金折完复利折
方法二:先补后减——(n+m)减m
4.永续年金现值
永续年金:收付次数为无穷大时的普通年金。
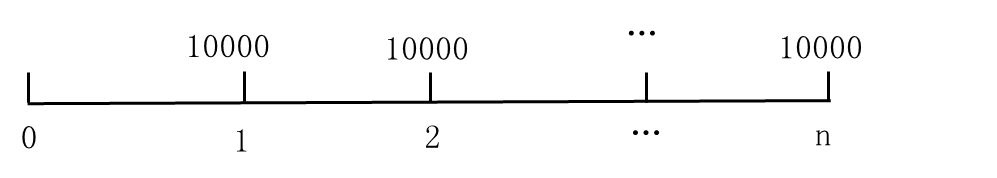
P=A×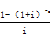 =A×(P/A,i,n)
=A×(P/A,i,n)

本讲小结
|
终值 |
普通年金 |
F=A×(F/A,i,n) |
|
预付年金 |
F=A×(F/A,i,n)×(1+i) =A×[(F/A,i,n+1)-1](补上再减去) |
|
|
递延年金 |
F=A×(F/A,i,n) |
|
|
永续年金 |
无 |
|
|
现值 |
普通年金 |
P=A×(P/A,i,n) |
|
预付年金 |
P=A×(P/A,i,n)×(1+i) =A×[(P/A,i,n-1)+1](遮上再加回) |
|
|
递延年金 |
P=A×(P/A,i,n)×(P/F,i,m) =A×[(P/A,i,n+m)-(P/A,i,m)] |
|
|
永续年金 |
P=A/i |


考呀呀
官方微信号

考呀呀APP
在线做题
微信扫一扫


加老师微信,备注领资料,免费领取