【知识点】最优存货量的确定(也叫做经济订货批量)
(一)经济订货基本模型
|
假设 |
（1）存货总需求量是已知常数； （2）不存在订货提前期，即可以随时补充存货； （3）货物是一次性入库； （4）单位货物成本为常数，无批量折扣； （5）库存储存成本与库存水平呈线性关系； （6）货物是一种独立需求的物品，不受其他货物影响； （7）不允许缺货，即无缺货成本，TCs为零 |
||
|
相关 成本 |
（1）储存变动成本 |
Q/2×KC |
|
|
（2）订货变动成本 |
D/Q×K |
|
|
|
总成本 |
总成本=Q/2×KC＋D/Q×K |
|
|
|
计算 |
|
|
|
|
|
|||
|
结论 |
|
||
【对比】
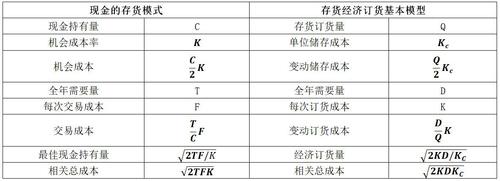
(二)经济订货基本模型的扩展
放宽经济订货基本模型的相关假设，就可以扩展经济订货模型，以扩大其适用范围。
1.再订货点
|
模型假设 |
（1）交货期不为零（放宽基本模型的第二个假设。虽不能“立即取得存货”，但到货是一次性的）（2）没有保险储备 |
|
计算公式 |
企业再次发出订货单时应保持的存货库存量＝平均交货时间×平均每日需求量 再订货点R=平均交货时间L×每日平均需用量d |
|
注意 |
再订货点R的单位是产品件数 |
|
经济订货量 |
订货提前期对经济订货量无影响（每次订货批量、订货次数、订货间隔时间等与瞬时补充相同） |
|
特点 |
企业在再订货点R明确的是，当存货还剩多少时就应当发出订单了 只是改变订货时间，没有改变经济订货量，也没改变批量相关成本 |
|
图示 |
|
2.存货陆续供应和使用模型
|
模型假设 |
陆续到货（放宽基本模型的第三个假设“货物是一次性入库”，其他条件不变） |
||
|
图示 |
|
||
|
相关成本 |
变动存储成本 |
Q |
每批订货数 |
|
P |
每天送货量 |
||
|
Q/P |
送货期 |
||
|
Q/P×d |
送货期内的生产耗用量 |
||
|
Q-Q/P×d |
最高库存量（货到齐时） |
||
|
（Q-Q/P×d）×1/2 |
平均库存量 |
||
|
Kc×（Q-Q/P×d）×1/2 |
变动存储成本 |
||
|
变动订货成本 |
D/Q×K |
变动订货成本 |
|
|
决策结果 |
|
|
|
|
影响因素 |
【备注】d受D的影响，如果每年经营天数不变的话，对D与d对最小相关总成本的影响不确定 |
||
(三)保险储备
|
原因 |
1.交货时间L可能延长 2.日需求量d可能增加 |
||
|
目标 |
设立保险储备，有保险储备成本；不设保险储备，可能会有缺货损失，找到最佳保险储备量，这是使保险储备量上的储存成本与缺货损失之和最低的保险储备量 |
||
|
假设 |
允许缺货（放宽基本模型的第七个假设：不允许缺货） |
||
|
指标重构 |
再订货点=交货时间×平均日需求＋保险储备 |
||
|
相关成本 |
缺货损失Cs=Ku×S×N Ku:每个订货周期每件产品缺货损失 S:平均缺货数量（缺货数量×缺货概率） N:每年订货次数 |
|
存储成本CB=B×Kc B:保险储备量（不需要乘1/2） Kc:单位存储成本 【思考】B为什么不需要乘1/2 |
|
相关总成本=TC（S、B）=KU×S×N＋B×KC |
|||
|
提示 |
教材只有交货期内需求增加的保险储备的决策例题。 对于因延误供货引起的缺货，教材提及一句话：可以通过估计延误时间和平均每日耗用量来计算增加的保险储备量，教材没有例题 |
||
考呀呀
官方微信号
考呀呀APP
在线做题
微信扫一扫
加老师微信，备注领资料，免费领取
微信公众号
学习更多干货
APP下载
扫码下载
学习中心
APP下载
