
【知识点】货币时间价值的计算
【所属章节】
第二章财务管理基础——第一节货币时间价值
【内容导航】
1.复利终值和现值
2.年金终值与年金现值
货币时间价值的计算
(一)复利终值和现值
1.复利终值
复利终值指现在的特定资金按复利计算方法,折算到将来某一时点的价值,或者说是现在的一定本金在将来一定时间,按复利计算的本金与利息之和,简称本利和。
2.复利现值
复利现值是指未来一时点的特定资金按复利计算方法,折算到现在的价值。或者说是为取得将来一定本利和,现在所需要的本金。
将复利终值计算公式F=P×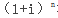 移项,可得:P=F×
移项,可得:P=F×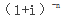
|
年金概念 |
年金,是指间隔期相等的系列等额收付款。通常记作A 例如,间隔期固定、金额相等的分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款以及每年相同的销售收入等,都属于年金 |
|
年金特点 |
(1)收付同方向,或者全部是现金流出,或者是现金流入; (2)各期金额相等; (3)间隔期(时间)相等 【提示】 (1)年金中收付的间隔时间不一定是1年,可以是半年、1个月等等 (2)年金中收付的起始时间可以是任何时点,不一定是年初到年末 |
|
年金类别 |
(1)普通年金:又称后付年金,是从现在开始,每期期末收款、付款的年金 (2)预付年金:又称即付年金或先付年金,是从现在开始,每期期初收款、付款的年金它和同期普通年金的区别在于整体前移一年 (3)递延年金:在第二期或第二期以后收付的年金 (4)永续年金:永续年金是普通年金的极限形式,当普通年金的收付次数为无穷大时即为永续年金 |
|
图示 |
|
1.普通年金终值的计算(已知年金A,求终值F)

2.年偿债基金的计算(已知终值求年金)
偿债基金是指为了在约定的未来某一时点清偿某笔债务或积聚一定数额的资金而必须分次等额形成的存款准备金。也就是为使年金终值达到既定金额的年金数额(即已知终值F,求年金A)。在普通年金终值公式中解出A,这个A就是偿债基金。
A=F×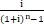
式中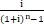 称作“偿债基金系数”,记作(A/F,i,n),上式也可写作:A=F×(A/F,i,n)
称作“偿债基金系数”,记作(A/F,i,n),上式也可写作:A=F×(A/F,i,n)
3.普通年金现值的计算
普通年金现值的计算实际上就是已知年金A,求普通年金现值P。
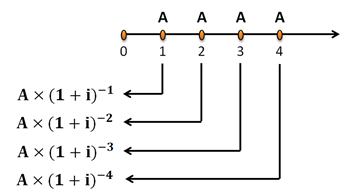

4.年资本回收额的计算(已知现值求年金)
年资本回收额是指在约定年限内等额回收初始投入资本的金额。年资本回收额的计算实际上是已知普通年金现值P,求年金A。
A=P×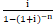
式中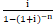 称作“资本回收系数”,记为(A/P,i,n)
称作“资本回收系数”,记为(A/P,i,n)
上式也可写作:A=P×(A/P,i,n),即:资本回收额=年金现值×资本回收系数
5.预付年金终值的计算
【定义方法】预付年金的终值,是指把预付年金每个等额A都换算成第n期期末的数值,再来求和。
【计算方法】有两个思路:
|
方法一 |
F=A(F/A,i,n)(1+i) |
预付年金终值系数=普通年金终值系数×(1+i) |
|
方法二 |
F=A[(F/A,i,n+1)-1] |
期数加1,系数减1 |
6.预付年金现值的计算
【定义方法】预付年金的现值就是把预付年金每个等额的A都换算成第一期期初的数值即第0期期末的数值,再求和。
【计算方法】有两个思路:
|
方法一 |
P=A(P/A,i,n)(1+i) |
预付年金现值系数=普通年金现值系数×(1+i) |
|
方法二 |
P=A[(P/A,i,n-1)+1] |
期数减1,系数加1 |
7.递延年金终值的计算
递延年金,是指第一次等额收付发生在第二期或第二期以后的年金。
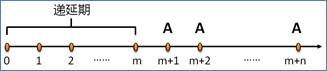
递延年金的终值计算与普通年金的终值计算一样,只是要注意期数。
F=A(F/A,i,n)
式中,“n”表示的是年金A的个数,与递延期无关。
8.递延年金现值的计算
【方法一】把递延期以后的年金套用普通年金公式求现值,这是求出来的现值是第一个等额收付前一期期末的数值,距离递延年金的现值点还有m期,再向前按照复利现值公式折现m期即可。
计算公式如下:P=A(P/A,i,n)×(P/F,i,m)
【方法二】把递延期每期期末都当作有等额的收付A,把递延期和以后各期看成是一个普通年金,计算出这个普通年金的现值,再把递延期多算的年金现值减掉即可。
P=A×[(P/A,i,m+n)-(P/A,i,m)]
【方法三】先求递延年金终值,再折现为现值。
P=A×(F/A,i,n)×(P/F,i,m+n)
9.永续年金现值的计算
永续年金是普通年金的极限形式,当普通年金的收付次数为无穷大时即为永续年金。永续年金的第一次等额收付发生在第1期期末。
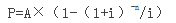
永续年金现值计算公式可通过普通年金现值公式导出:
当n→∞时,(1+i)-n的极限为零,故上式可写成:P=A/i。
永续年金因没有终止的时间,因此也就没有永续年金终值。
结论:
(1)复利终值和复利现值互为逆运算;
(2)复利终值系数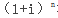 和复利现值系数
和复利现值系数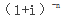 互为倒数。
互为倒数。
(二)年金终值与年金现值


考呀呀
官方微信号

考呀呀APP
在线做题
微信扫一扫


加老师微信,备注领资料,免费领取